а) Решите уравнение \( 6tg^2x-2cos^2x=cos2x \)
б) Укажите корни этого уравнения, принадлежащие отрезку [-2,5π;-0,5π]
Решение
\( 6tg^2x-2cos^2x=2cos^2x-1 \)
\( 6tg^2x=4cos^4x-1 \)
Вспомним: \( cos^2x+sin^2x=1 \) поделим на \( cos^2x≠0 \)
\( tg^2x+1=\frac{1}{cos^2x} \)
\( tg^2x=\frac{1}{cos^2x}-1 \)
подставим в уравнение
\( \frac{6}{cos^2x}-6=4cos^2x-1 \) умножим на \( cos^2x≠0 \)
и пусть \( cos^2x=t \), где \( t∈[0;1] \)
\( 6-4t^2=5t \)
\( t=-2 \) – не подходит
\( t=\frac{3}{4} \)
Делаем обратную замену
\( cos^2x=\frac{3}{4} \)
\( cosx=±\frac{\sqrt{3}}{2} \)
\( x=±\frac{\pi}{6}+2 \pi n \)
\( x=±\frac{5 \pi}{6}+2 \pi n \)
или
\( x=±\frac{\pi}{6}+\pi n \)
Б) Тут легко отобрать на окружности
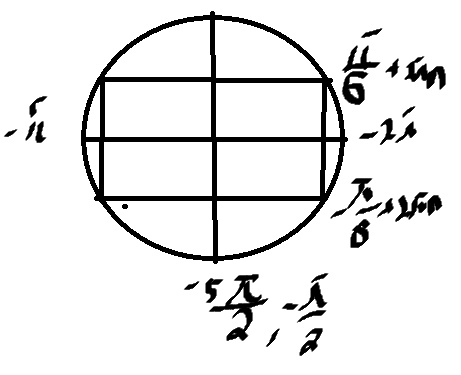
\( x=-2 \pi -\frac{\pi}{6}=-\frac{13 \pi}{6} \)
\( x=-2 \pi +\frac{\pi}{6}=-\frac{11 \pi}{6} \)
\( x=-\pi -\frac{\pi}{6}=-\frac{7 \pi}{6} \)
\( x=-\pi +\frac{\pi}{6}=-\frac{5 \pi}{6} \)
Ответ: а)\( x=±\frac{\pi}{6}+\pi n \) б) \( x=-\frac{13 \pi}{6}, -\frac{11 \pi}{6}, -\frac{7 \pi}{6}, -\frac{5 \pi}{6} \)
