а) Решите уравнение \( \frac{sin5x*cos3x-sin7x*cosx}{cos2x+sin2x}=0 \)
б) Укажите корни этого уравнения, принадлежащие промежутку (0,5π;π]
Решение
ОДЗ: \( sin2x+cos2x≠0 \) (разделим на \( cos2x≠0 \))
\( tg2x≠-1 \)
\( cos2x≠0 \)
\( x≠-\frac{\pi}{8}+\frac{\pi}{2}n \)
\( x≠\frac{\pi}{4}+\frac{\pi n}{2} \)
Воспользуемся формулой \( sina*sinb=0,5(sin(a+b)+sin(a-b)) \)
\( sin8x+sin2x-sin8x-sin6x=0 \)
\( sin2x-sin6x=0 \)
\( sin6x-sin2x=0 \)
\( 2sin2x*cos4x=0 \)
Получаем:
\( sin2x=0 \), \( x=\frac{\pi n}{2} \)
\( cos4x=0 \), \( x=\frac{\pi}{8}+\frac{\pi n}{4} \)
Отберем данные серии на ОДЗ
Получаем, что
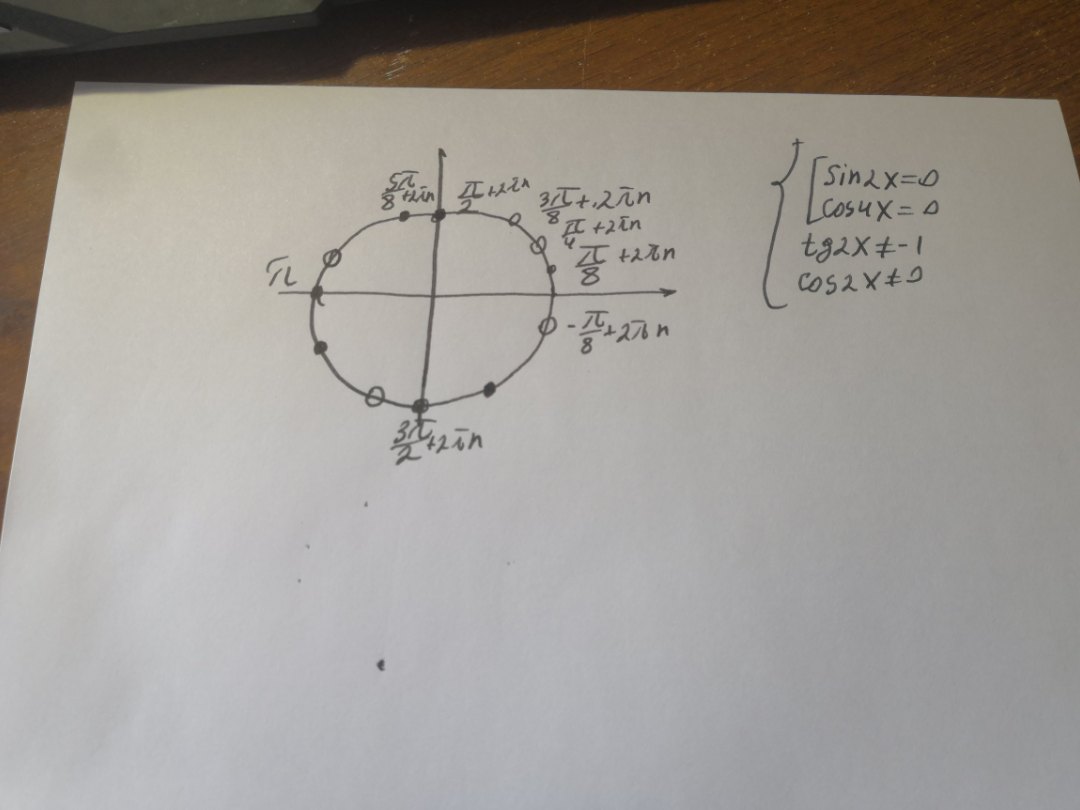
\( x=\frac{\pi}{8}+\frac{\pi n}{2} \)
\( x=\frac{\pi n}{2} \)
Б) Легко отобрать корни на окружности (только замечаем, что \( \frac{\pi}{2} \) – не входит в промежуток)
\( x=\frac{5 \pi}{8},\pi \)
Ответ: а) \( x=\frac{\pi}{8}+\frac{\pi n}{2} \), \( x=\frac{\pi n}{2} \) б) \( x=\frac{5 \pi}{8},\pi \)
