а) Решите уравнение \( log_{sinx}(3sinx-cos2x)=0 \)
б) Укажите корни этого уравнения, принадлежащие отрезку [-2/3π;π]
Решение
Начнем с ОДЗ:
\( sinx>0 \),\( sinx≠1 \) и
\( 3sinx-cos2x>0 \)
Предлагаю не решать все эти неравенства, а найти корни и проверить выполняются ли данные неравенства.
решаем само уравнение
\( 3sinx-1+2sin^2x=1 \)
\( 2sin^2x+3sinx-2=0 \)
решаем квадратное уравнение
\( sinx=-2 \) – такого быть не может
\( sinx=0,5 \)
\( x=(-1)^n\frac{π}{6}+πn \)
б) отберем корни на окружности
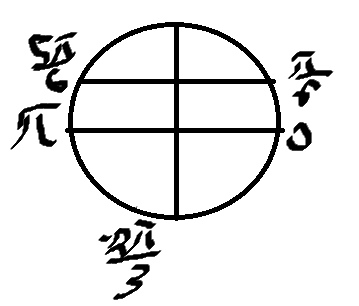
\( x=\frac{π}{6} \)
\( x=\frac{5π}{6} \)
Ответ: а) \( x=(-1)^n\frac{π}{6}+πn \) б) \( x=\frac{π}{6},\frac{5π}{6} \)
P.S Смотреть видео решение
