а) Решите уравнение \( 3*2^{cosx+3\sqrt{1-sin^2x}}+11*2^{2cosx}-34=0 \)
б) Укажите корни этого уравнения, принадлежащие отрезку [-0,5π;2,5π]
Решение
\( 3*2^{cosx+3\sqrt{1-sin^2x}}+11*2^{2cosx}-34=0 \)
\( 3*2^{cosx+3|cosx|}+11*2^{2cosx}-34=0 \)
Будет два случая, когда \( cosx≥0 \) и когда \( cosx<0 \)
1) Когда \( cosx≥0 \)
\( 3*2^{4cosx}+11*2^{2cosx}-34=0 \)
Пусть \( 2^{2cosx}=t \) \( t>0 \)
\( 3t^2+11t-34=0 \)
\( t=2 \)
\( t=-\frac{34}{6} \) – не подходит по ОДЗ
\( 2^{2cosx}=2 \)
\( cosx=0,5 \)
\( x=±\frac{π}{3}+2πn \)
б) Отберем корни на окружности
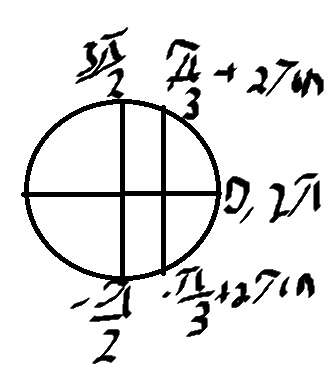
\( x=±\frac{π}{3} \)
\( x=2π-\frac{π}{3}=\frac{5π}{3} \)
\( x=2π+\frac{π}{3}=\frac{7π}{3} \)
2) Когда \( cosx<0 \)
Делаем ту же замену, решаем квадратное уравнение и получаем, что ни один из корней нам не подходит. Разберите этот случай самостоятельно. Если будет непонятно, то пишите в комментарии ниже.
Ответ: а) \( x=±\frac{π}{3}+2πn \) б) \( x=±\frac{π}{3},\frac{5π}{3},\frac{7π}{3} \)
