а) Решите уравнение √21 cosx*ctgx-√7cosx-√7ctgx=0
б) Укажите корни этого уравнения, принадлежащие отрезку [-π;π]
Решение
ОДЗ: \( sinx≠0 \), \( x≠πn \)
\( \sqrt{21}cosx*ctgx-\sqrt{7}cosx-\sqrt{7}ctgx=0 \)
\( \sqrt{21}cosx*\frac{cosx}{sinx}-\sqrt{7}cosx-\sqrt{7}\frac{cosx}{sinx}=0 \)
\( \sqrt{7}cosx(\sqrt{3}\frac{cosx}{sinx}-1-\frac{1}{sinx})=0 \)
\( cosx=0 \) значит \( x=\frac{π}{2}+πn \)
\( \sqrt{3}\frac{cosx}{sinx}-1-\frac{1}{sinx}=0 \)
\( \sqrt{3}cosx-sinx=1 \) – решим это уравнение с помощью метода введения вспомогательного угла.
Поделим его на \( \sqrt{(\sqrt{3})^2+1^2}=2 \)
\( \frac{\sqrt{3}}{2}cosx-0,5sinx=\frac{1}{2} \)
Пусть \( sin\frac{π}{3}=\frac{\sqrt{3}}{2} \), и \( cos\frac{π}{3}=\frac{1}{2} \)
\( sin\frac{π}{3}cosx-cos\frac{π}{3}sinx=0,5 \)
\( sin(\frac{π}{3}-x)=0,5 \)
\( sin(x-\frac{π}{3})=-0,5 \)
\( x-\frac{π}{3}=(-1)^{n+1}\frac{π}{6}+πn \)
\( x=\frac{π}{3}+(-1)^{n+1}\frac{π}{6}+πn \)
или распишем на две серии корней
\( x=\frac{π}{6}+2πn \)
\( x=-\frac{π}{2}+2πn \)
Еще не забываем, про \( x=\frac{π}{2}+πn \)
Б) Отберем на окружности
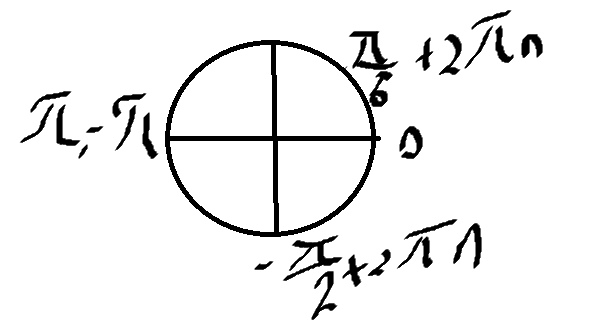
\( x=-\frac{π}{2} \)
\( x=\frac{π}{6} \)
\( x=\frac{π}{2} \)
Ответ: а) \( x=\frac{π}{6}+2πn \), \( x=\frac{π}{2}+πn \)б) \( x=-\frac{π}{2},\frac{π}{6},\frac{π}{2} \)
