а) Решите уравнение \( \frac{sin3x}{1+2cos2x}=0 \)
б) Укажите корни этого уравнения, принадлежащие промежутку [-π;π)
Решение
ОДЗ:
\( 1+2cos2x≠0 \)
\( cos2x≠-0,5 \)
\( 2x≠±\frac{2π}{3}+2πn \)
\( x≠±\frac{π}{3}+πn \)
Решаем само уравнение
\( sin3x=0 \)
\( x=\frac{πn}{3} \)
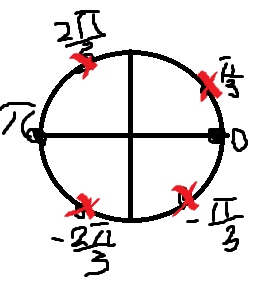
С учетом ОДЗ получаем, что \( x=πn \)
Б) Тут все легко, с помощью единичной окружности получаем ответ
Ответ: а) \( x=πn \) б) \( x=-π,0 \)
