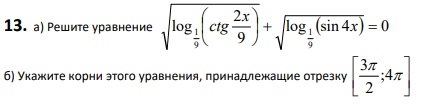
Решение
Уравнение страшное на первый взгляд, да и фиг знает как его решать.
Но тут же сумма корней, которая равна нулю. Все, после этой фразы, уравнение уже решено.
Сумма двух корней равна нулю, значит и сами эти корни должны равняться нулю, а по другому никак.
То есть логарифмы должны быть нулями, а это возможно только тогда, когда аргументы равны 1
\( ctg(2x/9)=1 \)
\( sin4x=1 \)
\( x=9(\frac{π}{8}+\frac{πn}{2}) \)
\( x=\frac{π}{8}+\frac{πn}{2} \)
Объедияем серии и получаем просто \( x=9(\frac{π}{8}+\frac{πn}{2}) \)
Б) Отобрать корни на окружности я не рискну, поэтому отберем с помощью двойного неравенства
\( \frac{3π}{2}≤9(\frac{π}{8}+\frac{πn}{2})≤4π \)
Решая его получаем \( \frac{3}{36}≤n≤\frac{23}{36} \)
нету целых n(
То есть нету корней, принадлижащих этому промежутку
Ответ: а) \( x=9(\frac{π}{8}+\frac{πn}{2}) \) б) нет корней.
P.S Если решение было непонятно, то оставляйте комментарии ниже, я или кто-то другой обязательно ответит:)
