а) Решите уравнение (1+√3)/2sin2x=(√3-1)cos^2x+1
б) Укажите корни этого уравнения, принадлежащие отрезку [π;1,5π]
Решение
\( (1+\sqrt{3})sinxcosx-(\sqrt{3}-1)cos^2x-1=0 \)
\( (1+\sqrt{3})sinxcosx-(\sqrt{3}-1)cos^2x-sin^2x-cos^2x=0 \)
\( (1+\sqrt{3})sinxcosx-\sqrt{3}cos^2x-sin^2x=0 \)
Делим все на \( cos^2x≠0 \)
\( tg^2x-tgx-\sqrt{3}tgx+\sqrt{3}=0 \)
\( (tgx-1)(tgx-\sqrt{3})=0 \)
\( tgx=1 \)
\( tgx=\sqrt{3} \)
\( x=\frac{π}{4}+πn \)
\( x=\frac{π}{3}+πn \)
Отберем корни на единичной окружности
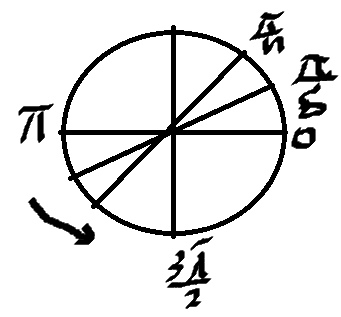
\( x=\frac{π}{4}+π=\frac{5π}{4} \)
\( x=\frac{π}{3}+π=\frac{4π}{3} \)
Ответ: а) \( x=\frac{π}{4}+πn \) \( x=\frac{π}{6}+πn \)б) \( x=\frac{4π}{3},\frac{5π}{4} \)
