13. а) Решите уравнение √10cosx-√(4cosx-cos2x)=0
б) Укажите корни этого уравнения, принадлежащие промежутку (-π/3;2π]
Решение
\( \sqrt{10}cosx=\sqrt{4cosx-cos2x} \)
Напишем ОДЗ
\( cosx≥0 \) – этого достаточно.(1)
Возведем обе части в квадрат
\( 10cos^2x=4cosx-cos2x \)
\( 10cosx^2x=4cosx-cos^2x+sin^2x=4cosx-2cos^2x+1 \)
\( 12cos^2x-4cosx-1=0 \)
Пусть \( cosx=t \), где \( -1≤t≤1 \) (2)
\( 12t^2-4t-1=0 \)
\( t=-1/6 \)
\( t=1/2 \)
Делаем обратную замену и проверяем выполняются ли условия (1) и (2).
Условие (2) выполняется для обоих корней, но (1) только для одного, поэтому
\( cosx=1/2 \)
\( x=±\frac{π}{3}+2πn \)
Б) Отберем корни на окружности
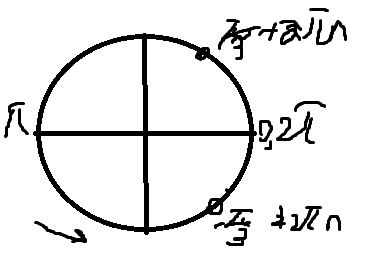
\( x=\frac{π}{3} \)
\( x=2π-\frac{π}{3}=\frac{5π}{3} \)
Ответ: а) \( x=±\frac{π}{3}+2πn \)n-целые числа, б) \( x=2π-\frac{π}{3}=\frac{5π}{3} \)
