а) Решите уравнение \( 3*2^{cosx+3\sqrt{1-sin^2x}}+11*2^{2cosx}-34=0 \)
б) Укажите корни этого уравнения, принадлежащие отрезку [-1.5π;0,5π]
Решение
У нас тут 2 случая когда раскрываем cos с плюсом и минусом, но нам достаточно рассмотреть только с +, т.к с – не имеет смысла, попробуйте доказать это самостоятельно.
\( 3*2^{cosx+3\sqrt{1-sin^2x}}+11*2^{2cosx}-34=0 \)
\( 3*2^{cosx+3cosx}+11*2^{2cosx}-34=0 \)
\( 3*2^{4cosx}+11*2^{2cosx}-34=0 \)
Сделаем замену на \( 2^{2cosx}=t \),\( t>0 \)
\( 3t^2+11t-34=0 \)
\( t=-17/3 \) – не подходит под условие
\( t=2 \)
\( 2^{2cosx}=2 \)
\( 2cosx=1 \)
\( cosx=0,5 \)
\( x=±\frac{\pi}{3}+2\pi n \)
Б)
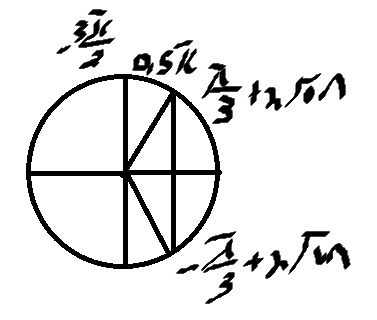
\( x=-\frac{\pi}{3} \)
\( x=\frac{\pi}{3} \)
Ответ: а) \( x=±\frac{\pi}{3}+2\pi n \) б) \( x=-\frac{\pi}{3},\frac{\pi}{3} \)
