а) Решите уравнение \( (\frac{6}{5})^{cos3x}+(\frac{5}{6})^{cos3x}=2 \)
б) Укажите корни этого уравнения, принадлежащие отрезку [4π;4,5π)
Решение
а) Тут нужно взгянуть внимательно на само уравнение и не пытаться как-то преобразовывать.
Мы должны получить 2. Очевидно, что степень должна быть ноль, тогда будет \( (\frac{6}{5})^0+(\frac{5}{6})^0=2 \) – что верно
То есть \( cos3x=0 \)
\( 3x=\frac{π}{2}+πn \)
\( x=\frac{π}{6}+\frac{πn}{3} \), где n – целые
б) Тут можно отобрать на окружности
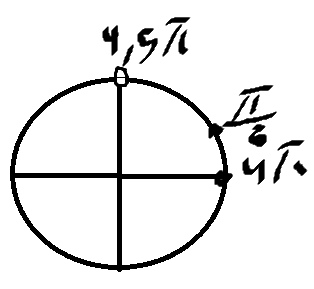
\( x=4π+\frac{π}{6}=\frac{25π}{6} \)
Ответ: а) \( x=\frac{π}{6}+\frac{πn}{3} \), где n – целые, б) \( x=4π+\frac{π}{6}=\frac{25π}{6} \)
