Дано уравнение \( 2*8^{cos(\frac{3π}{2}+x)}=(\frac{1}{2})^{cos2x} \)
А) Решите уравнение.
Б) Укажите корни этого уравнения, принадлежащие отрезку [2π;3,5π]
Решение
А) Сведем все к одному основанию и воспользуемся формулой привидения.
\( 2*2^{3sinx}=2^{-cos2x} \)
\( 2^{1+3sinx}=2^{-cos2x} \)
\( cos2x+3sinx+1=0 \)
\( cos^2x-sin^2x+3sinx+cos^2x+sin^2x=0 \)
\( 2cos^2x+3sinx=0 \)
\( 2-2sin^2x+3sinx=0 \)
Пусть \( sinx=t \), где -1≤t≤1
\( 2t^2-3t-2=0 \)
\( t=2 \) – не подходит по условию
\( t=-0,5 \)
\( sinx=-0,5 \)
\( x=(-1)^{n+1}\frac{π}{6}+πn \)
Б) отберем корни на окружности
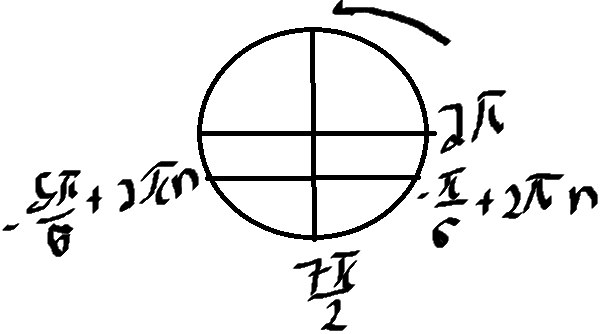
\( x=3π+\frac{π}{6}=\frac{19π}{6} \)
Ответ: а) \( x=(-1)^{n+1}\frac{π}{6}+πn \) б) \( x=\frac{19π}{6} \)
