Дано уравнение \( \frac{1}{cos2x*cosx}=\frac{1}{sin2x*sinx} \)
А) Решите уравнение.
Б) Укажите корни этого уравнения, принадлежащие отрезку [-2π;-0,5π]
Решение
ОДЗ:
\( cos2x≠0 \), \( cosx≠0 \), \( sinx≠0 \), \( sin2x≠0 \)/
“Перевернем” это уравнение (если правильно расписывать, то умножим на cos2x*cosx и sin2x*sinx на ОДЗ).
\( cos2x*cosx=sin2x*sinx \)
\( cos2x*cosx=2sin^2x*cosx \)
\( cosx(cos2x-2sin^2x)=0 \)
\( cosx=0 \) – не подходит под ОДЗ
\( cos2x-2sin^2x=0 \)
\( cos^2x-3sin^2x=0 \)
\( 1-4sin^2x=0 \)
\( sinx=±\frac{1}{2} \)
\( x=(-1)^n\frac{π}{6}+πn \)
\( x=(-1)^{n+1}\frac{π}{6}+πn \)
Или можно записать \( x=±\frac{π}{6}+πn \)
Б) Отберем корни на окружности
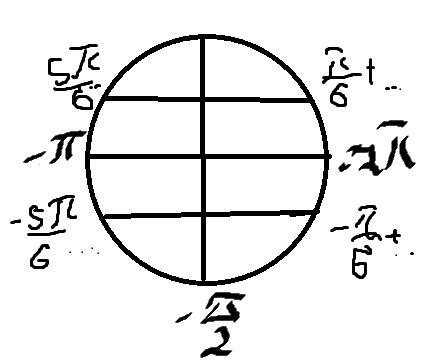
\( x=-2π+\frac{π}{6}=-\frac{11π}{6} \)
\( x=-π-\frac{π}{6}=-\frac{7π}{6} \)
\( x=-π+\frac{π}{6}=-\frac{5π}{6} \)
Ответ: а) \( x=±\frac{π}{6}+πn \) Б) \( x=-\frac{11π}{6}=-\frac{7π}{6}=-\frac{5π}{6} \)
