Решение
\( \frac{5}{sin^2x}+\frac{7}{sinx}-6=0 \)
Умножим на sin^2x он не равен нулю по основному тригонометрическому тождеству.
\( 5+7sinx-6sin^2x=0 \)
Пусть sinx=t, -1≤t≤1
\( 6t^2-7t-5=0 \)
\( t=-0,5 \)
\( t=\frac{5}{3} \) – не подходит
\( sinx=-0,5 \)
\( x=(-1)^{n+1}\frac{π}{6}+πn \)
Б) найдем корни на единичной окружности
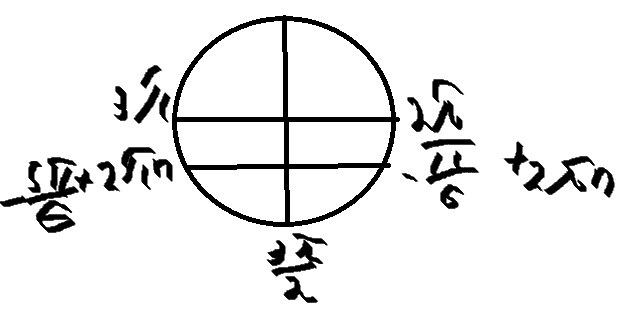
\( x=2π-\frac{π}{6}=\frac{11π}{6} \)
Ответ: А) \( x=(-1)^{n+1}\frac{π}{6}+πn \) Б) \( x=\frac{11π}{6} \)
