а) Решите уравнение \( cos2x+\sqrt{2}*cos(x+\frac{5π}{4})=sinx \)
Б) Найдите все корни этого уравнения, принадлежащие отрезку \( [6π;\frac{15π}{2}] \)
Решение
\( cos2x+\sqrt{2}(cosx*cos(\frac{5π}{4})-sinx*sin(\frac{5π}{4}))=sinx \)
\( cos2x+\sqrt{2}(cosx*cos(π+\frac{π}{4})-sinx*sin(π+\frac{π}{4}))=sinx \)
\( cos2x-\sqrt{2}*cosx*cos(\frac{π}{4})+\sqrt{2}sinx*sin(\frac{π}{4})=sinx \)
\( cos2x-cosx+sinx=sinx \)
\( cos^2x-sin^2x-cosx=0 \)
\( 2cos^2x-cosx-1=0 \)
Пусть cosx=t, где |t|≤1
\( 2t^2-t-1=0 \)
\( t=-0,5 \)
\( t=1 \)
Значит
\( cosx=-0,5 \), \( x=±\frac{2π}{3}+2πn \)
\( cosx=1 \), \( x=2πn \)
Б) Отберем корни на окружности
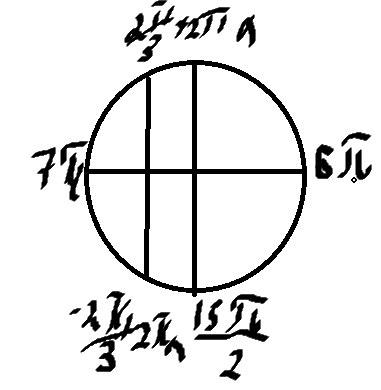
\( x=6π \)
\( x=6π+\frac{2π}{3}=\frac{20π}{3} \)
\( x=7π+\frac{π}{3}=\frac{22π}{3} \)
Ответ: а) \( x=±\frac{2π}{3}+2πn \), \( x=2πn \) Б) \( x=6π,\frac{20π}{3}, \frac{22π}{3}\),
