а) Решите уравнение \( \frac{cos2x-cos4x-4sin3x-2sinx+4}{2sinx-1}=0 \)
Б) Найдите корни, принадлежащие промежутку \( [-π;\frac{3π}{2}] \)
Решение
ОДЗ \( sinx≠0,5 \)
\( x≠\frac{π}{6}+2πn \)
\( x≠\frac{5π}{6}+2πn \)
Решаем само уравнение, преобразуем его
\( 2sin3x*sinx-4sin3x-2sinx+4=0 \) (\( cos2x-cos4x=-2sin\frac{2x+4x}{2}*sin\frac{2x-4x}{2}=2sin3x*sinx \))
\( 2sin3x(sinx-2)-2(sinx-2)=0 \)
\( (sin3x-1)(sinx-2)=0 \)
\( sinx=2 \) – нет решений
\( sin3x=1 \), \( 3x=\frac{π}{2}+2πn \)
\( x=\frac{π}{6}+\frac{2π}{3} \)
Если n=0, то \( x=\frac{π}{6} \) – не подходит под ОДЗ
Если n=1, то \( x=\frac{5π}{6} \) – не подходит под ОДЗ
Если n=2, то \( x=\frac{3π}{2} \) – подходит
Если n=3, то опять же x не подходит под ОДЗ
Таким образом, \( x=\frac{3π}{2}+2πn \)
Б) Отберем корни на окружности
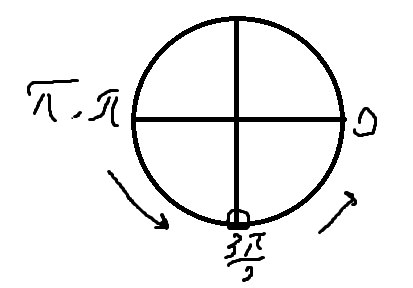
\( x=-\frac{π}{2} \)
Ответ: а) \( x=\frac{3π}{2}+2πn \) Б) \( x=-\frac{π}{2} \)
