А) Решите уравнение \( sinx+cos(5x-4,5π)=\sqrt{3}sin(3x+π) \)
Б) Найдите корни, принадлежащие отрезку [-π;0,5π]
Решение
\( sinx+cos(4,5π-5x)=\sqrt{3}sin(π+3x) \)
\( sinx+sin5x=-\sqrt{3}sin3x \)
\( 2sin3x*cos2x=-\sqrt{3}sin3x \)
\( sin3x(2cos2x+\sqrt{3})=0 \)
\( sin3x=0 \)
\( cos2x=-\frac{\sqrt{3}}{2} \)
Значит
\( x=\frac{πn}{3} \)
\( x=±\frac{5π}{12}+πn \)
Б) Отбирать корни на окружности проблематично, да и пропустить корни можно, в данном случае лучше через двойное неравенство. Решение на фотографии, чтобы увеличить кликните по фотке:)
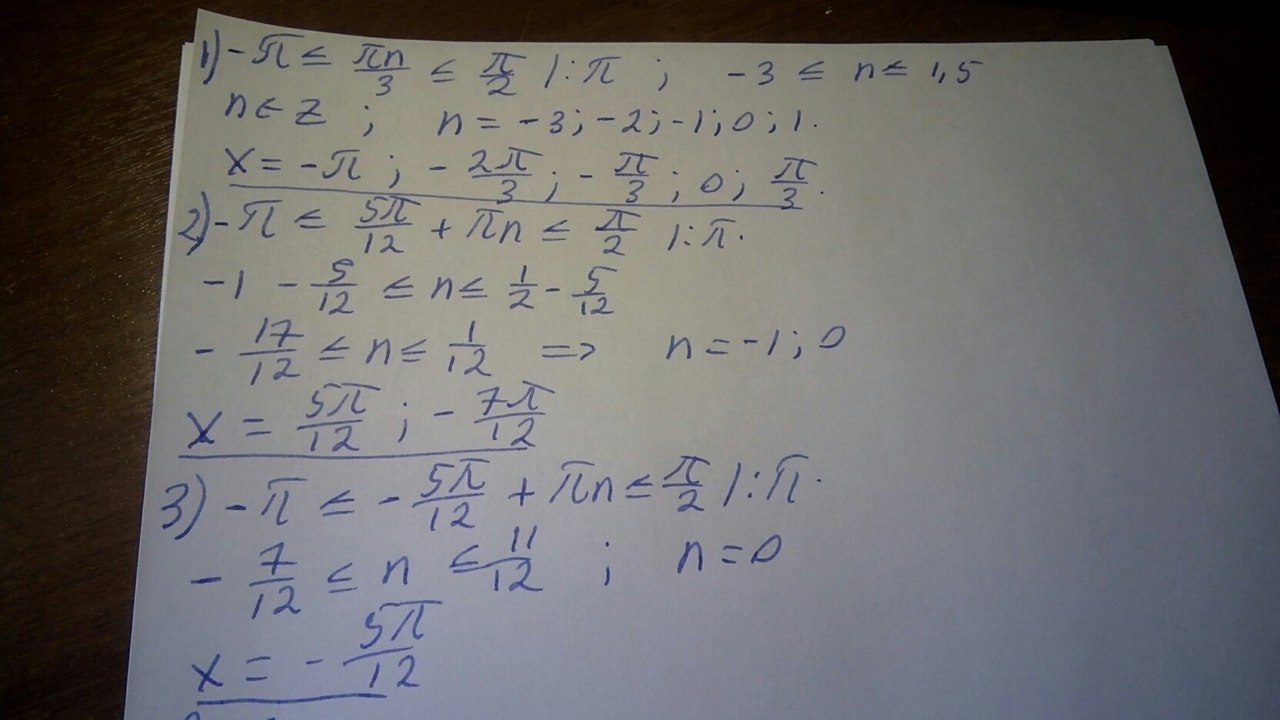
Ответ: а) \( x=\frac{πn}{3} \), \( x=±\frac{5π}{12}+πn \) Б) \( x=-π;-\frac{2π}{3};-\frac{7π}{12};-\frac{5π}{12};-\frac{π}{3};0;\frac{π}{3};\frac{5π}{12} \)
