Дано уравнение √sin2x=2^(1/4)*√cosx
А) Решите уравнение.
Б) Укажите корни этого уравнения, принадлежащие отрезку [-1,5π;0]
Решение
А) ОДЗ, \( cosx≥0 \) (это 1 и 4 четверть на тригонометрической окружности) и \( sin2x≥0 \) (это 1 и 3 четверть)
\( πn≤x≤\frac{π}{2}+πn \)
\( -\frac{π}{2}+2πn≤x≤\frac{π}{2}+2πn \)
Объединяем
Получаем, \( 2πn≤x≤\frac{π}{2}+2πn \), x∈ {\( -\frac{π}{2}+2πn \)}
Теперь мы имеем право возвести все в квадрат
\( sin2x=\sqrt{2}cosx \)
\( 2sinx*cosx=\sqrt{2}cosx \)
\( cosx(2sinx-\sqrt{2})=0 \)
\( cosx=0 \)
\( sinx=\frac{\sqrt{2}}{2} \)
\( x=\frac{π}{2}+πn \)
\( x=\frac{π}{4}+2πn \)
\( x=\frac{3π}{4}+2πn \) – не попадает в ОДЗ (эта точка в 2 четверти)
Б) Отберем корни на окружности
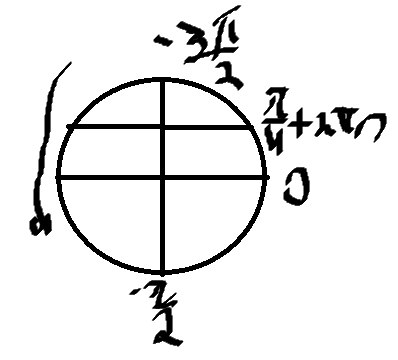
\( x=-\frac{3π}{2} \)
\( x=-\frac{π}{2} \)
Ответ: \( x=\frac{π}{2}+πn \), \( x=\frac{π}{4}+2πn \), Б) \( x=-\frac{3π}{2} \) \( x=-\frac{π}{2} \)
