А) Решите уравнение cos2(x+π/3)+4sin(x+π/3)=2.5
Б) Найдите корни, принадлежащие отрезку [-0,5π;π]
Решение
Пусть (x+π/3)=t
Тогда \( cos2t+4sint=2.5 \)
\( cos^2t-sin^2t+4sint=2.5 \)
\( 1-2sin^2t+4sint-2.5=0 \)
\( 2sin^2t-4sint+1.5=0 \)
\( 4sin^2t-8sint+3=0 \)
\( sint=0.5 \)
\( sint=1.5 \) – тут решений нету, т.к область значений синуса от -1 до 1
\( t=(-1)^n\frac{π}{6}+πn \)
Делаем обратную замену
\( x+π/3=(-1)^n\frac{π}{6}+πn \)
\( x=(-1)^n\frac{π}{6}-\frac{π}{3}+πn \)
Для удобства распишем две серии корней
\( x=\frac{π}{6}-\frac{π}{3}+2πn \)
\( x=\frac{5π}{6}-\frac{π}{3}+2πn \)
\( x=-\frac{π}{6}+2πn \)
\( x=\frac{π}{2}+2πn \)
Б) отберем корни на окружности
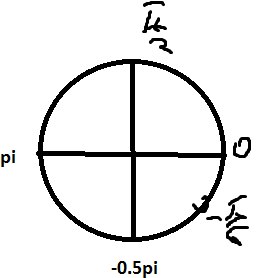
Ответ: а)\( x=-\frac{π}{6}+2πn \), \( x=\frac{π}{2}+2πn \)Б) \( x=-\frac{π}{6} \), \( \frac{π}{2} \)
