А) Решите уравнение 3sin^2x-cos(9π/2-x)*sin(3π/2+x)-2=0
Б) Найдите корни, принадлежащие отрезку [3π;4π]
Решение видео
Решение текстовое
Преобразуем уравнение
\( 3sin^2x+sinx*cosx-2=0 \)
\( 2sin^2x+2cos^2x=2 \)
\( 3sin^2x+sinx*cosx-2cos^2x-2sin^2x=0 \)
\( sin^2x+sinx*cosx-2cos^2x=0 \) поделим на cos^2x не равным нулю
\( tg^2x+tgx-2=0 \) решаем как обычно через замену
\( tgx=-2 \), \( x=-arctg2+πn \)
\( tgx=1 \), \( x=π/4+πn \)
Б) отберем с помощью окружности
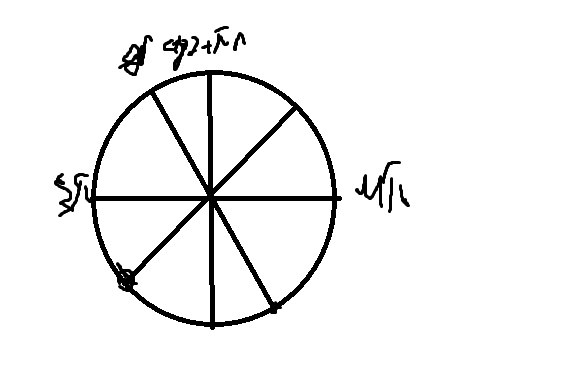
\( x=3π+π/4=13π/4 \)
\( x=4π-arctg2 \)
Ответ: \( x=π/4+πn \), \( x=-arctg2+πn \), \( x=3π+π/4=13π/4 \),\( x=4π-arctg2 \)
