а) Решите уравнение: sin^2x+3x^2cosx+3x^2=0
б) Укажите корни этого уравнения, принадлежащие отрезку [-0.5pi;pi]
Решение
а) \( 1-cos^2x+3x^2*cosx+3x^2=0 \)
\( (1-cosx)(1+cosx)+3x^2(cosx+1)=0 \)
\( (cosx+1)(1-cosx+3x^2)=0 \)
\( cosx=-1 \) значит \( x=π+2πn \)
\( cosx=1+3x^2 \) – мы должны подобрать такое x чтобы это уравнение было тождественным.
Область значений косинуса от -1 до 1.
Очевидно, что если x=0, то \( cos0=1-0 \) – что верно, т.к cos0=1
Б) Отберем корни на окружности
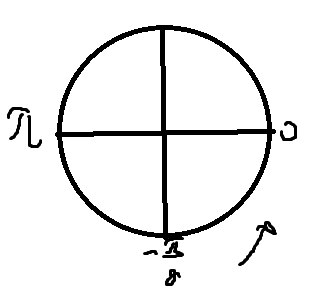
\( x=0 \)
\( x=π \)
Ответ: А) \( x=π+2πn \), \( x=0 \) Б) \( x=0 \), \( x=π \)
