Дано уравнение sin7x-cos6x-sin5x=2sinx+5
А) Решите уравнение.
Б) Укажите корни этого уравнения, принадлежащие отрезку [-7π;-5π]
Решение
Преобразуем уравнение
\( 2cos6x*sinx-cos6x=2sinx+5 \)
\( 2cos6x*sinx-cos6x-2sinx-5=0 \)
Тут на множители никак не разложить
Поэтому решим методом оценки
Область значений и синуса и косинуса от -1 до 1
Ну не трудно догадаться, что
\( sinx=-1 \)
\( cos6x=-1 \)
Тогда получим
\( 2+1+2-5=0 \) – что верно.
\( x=-\frac{π}{2}+2πn \) –
\( x=\frac{π}{6}+\frac{πn}{3} \)
Объединяем серии корней
\( x=-\frac{π}{2}+2πn \) (можно подставить допустим pi/2 в уравнение и убедиться, что оно равно нулю)
б) Отберем корни
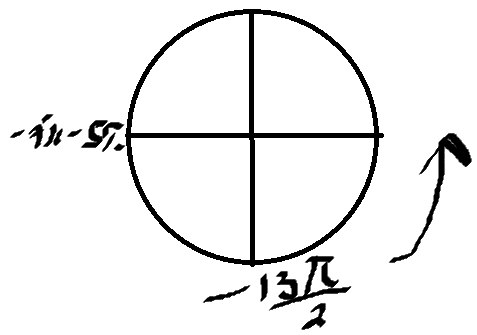
\( x=-6.5π \)
Ответ: а) \( x=-\frac{π}{2}+2πn \) б) \( x=-6.5π \)
