а) Решите уравнение: \( \frac{2-3sinx-3cos2x}{6x^2-πx-π^2}=0 \)
б) Укажите корни этого уравнения, принадлежащие отрезку \( [-\frac{π}{2};\frac{2π}{3}] \)
Решение
Найдем ОДЗ
\( 6x^2-πx-π^2≠0 \) – решим это уравнение относительно x (чтобы увеличить кликните по фотке)
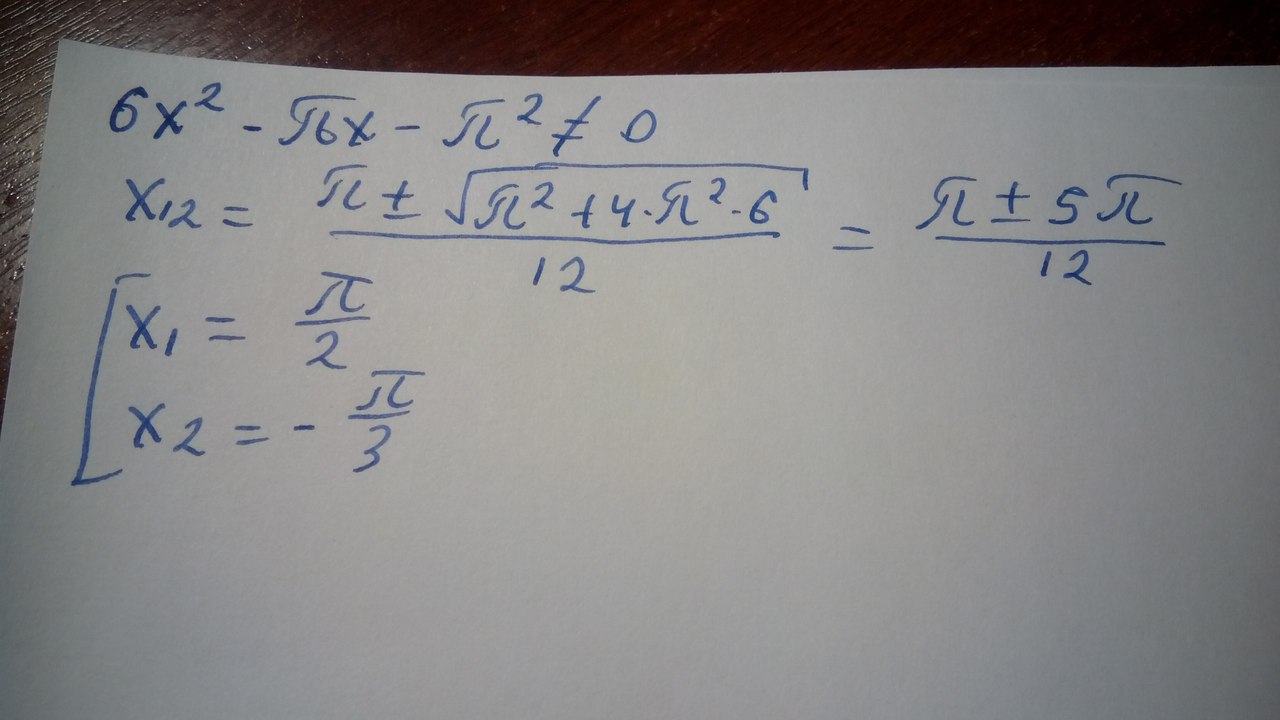
Теперь решаем само уравнение
\( 2-3sinx-(1-2sin^2x)=0 \)
\( 2sin^2x-3sinx+1=0 \)
\( sinx=1 \) и \( sinx=\frac{1}{2} \)
\( x=\frac{π}{2}+2πn \) и \( x=(-1)^m\frac{π}{6}+mn \)
Так как выкалывается точка \( \frac{π}{2} \), то \( n \) – это все целые числа, кроме нуля
\( m \)- все целые числа
б) Отберем корни на окружности
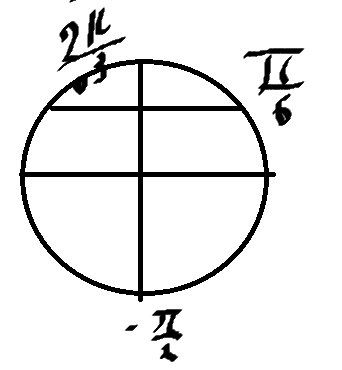
\( x=\frac{π}{6} \)
Ответ: \( x=\frac{π}{2}+2πn \) и \( x=(-1)^m\frac{π}{6}+mn \), \( n \) – это все целые числа, кроме нуля\( m \)- все целые числа, б) \( x=\frac{π}{6} \)
