Решите уравнение: \( 7sin(2x-\frac{5π}{2})+9cosx+1=0 \)
б) Укажите корни этого уравнения, принадлежащие отрезку \( [-\frac{3π}{2};\frac{π}{3}] \)
Решение
\( -7sin(\frac{5π}{2}-2x) +9cosx+1=0\)
\( -cos2x+9cosx+1=0 \)
\( -7cos^2x+7sin^2x+9cosx+1=0 \)
\( -14cos^2x+9cosx+8=0 \)
\( 14cos^2x-9cosx-8=0 \)
Делаем замену на cosx, решаем квадратное уравнение, находим корни и отбрасываем лишний.
\( cosx=-0.5 \)
\( x=±\frac{2π}{3}+2πn \)
б) Отберем корни на окружности
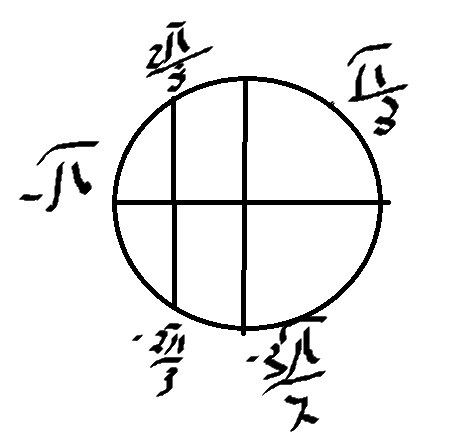
\( x=-π-\frac{2π}{3}=-\frac{4π}{3} \)
\( x=-\frac{2π}{3} \)
Ответ: а) \( x=±\frac{2π}{3}+2πn \) б)\( x=-π-\frac{2π}{3}=-\frac{4π}{3} \)\( x=-\frac{2π}{3} \)
