Дано уравнение 8^x+3=3*4^x+2^x
а) Решите уравнение.
б) Укажите корни этого уравнения, принадлежащие отрезку [-0.5;1.5]
Решение
Пусть \( 2^x=t \), \( t>0 \)
\( t^3-3t^2-2t+3=0 \) – тут конечно очевидно, что корень \( t=1 \)
Поделим уравнение на \( t-1 \) и соответственно разложим на множители
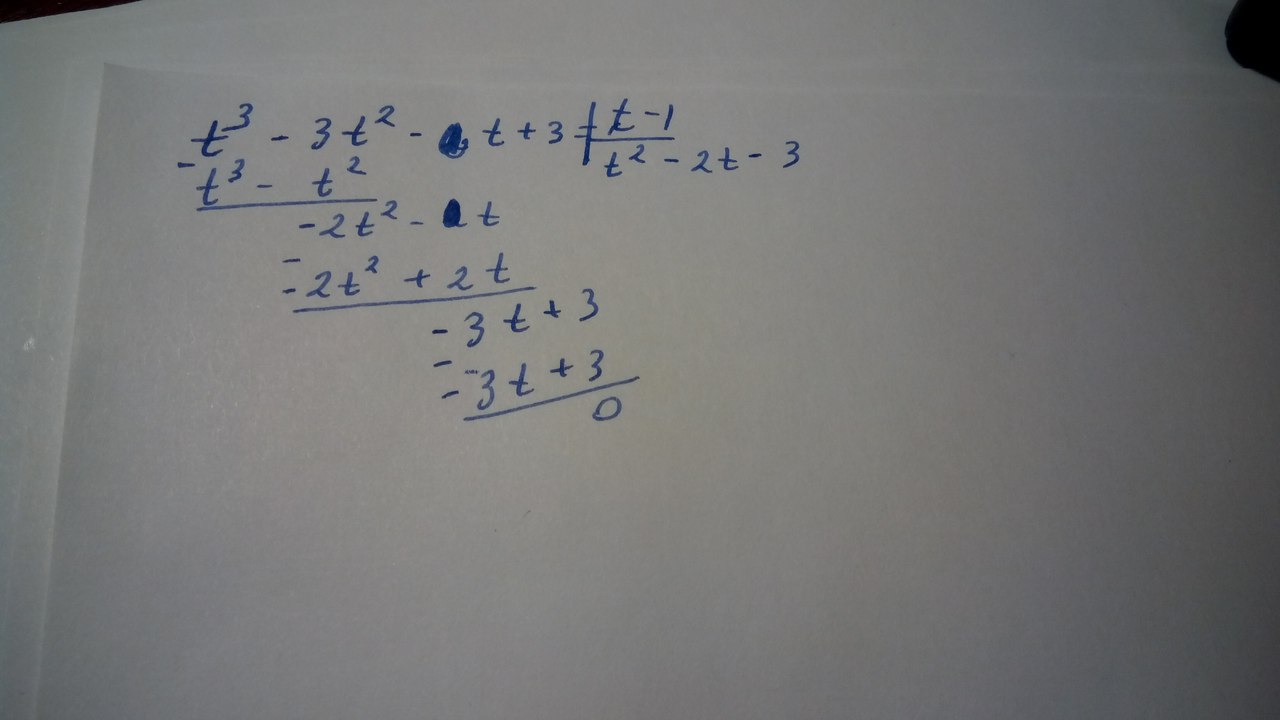
\( (t-1)(t^2-2t-3)=0 \)
\( (t-1)(t+1)(t-3)=0 \)
\( t=1 \) значит \( 2^x=1 \) получаем \( x=0 \)
\( t=-1 \) значит \( 2^x=-1 \) нет решений
\( t=3 \) значит \( 2^x=3 \) и \( x=log2(3)=log_{2}\sqrt{9} \)
б) Корень \( x=0 \) – очевидно подходит
\( 1.5=log_{2}2^{1.5}=log_{2}\sqrt{8} \)
Значит корень \( x=log_{2}3 \) нам не подходит
Ответ: \( x=0, x=log_{2}3 \) Б) \( x=0 \)
