а) Решите уравнение cos3x=√3sin4x+cos5x
б) Укажите корни этого уравнения, принадлежащие отрезку [0.5π;π]
Решение
\( cos3x-cos5x=\sqrt{3}sin4x \)
\( -2sin(\frac{3x+5x}{2})*sin(\frac{3x-5x}{2}) \)
\( 2sin4x*sinx=\sqrt{3}sin4x \)
\( sin4x(2sinx-\sqrt{3})=0 \)
Значит
\( sin4x=0 \) и \( x=\frac{πn}{4} \)
\( sinx=\frac{\sqrt{3}}{2} \) и \( x=(-1)^n\frac{π}{3}+πn \)
Теперь пункт Б
\( x=(-1)^n\frac{π}{3}+πn \)
\( x=\frac{2π}{3} \)
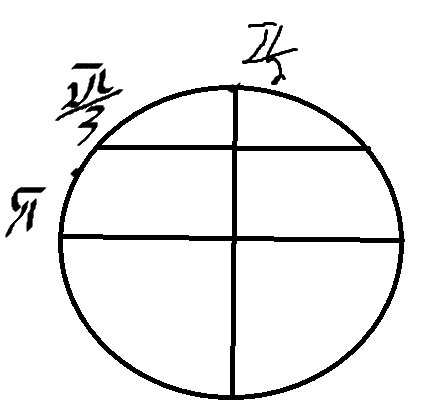
\( \frac{π}{2}≤\frac{πn}{4}≤π \) отсюда \( 2≤n≤4 \)значит \( n=2,3,4 \)
\( x=\frac{π}{2} \)
\( x=\frac{3π}{4} \)
\( x=π \)
Ответ: а) \( x=\frac{πn}{4} \) , \( x=-(1)^n*\frac{π}{3}+πn \) б)\( x=\frac{π}{2}, \frac{3π}{4}, \frac{2π}{3}, π \)
