а) Решите уравнение \( \frac{25sin2x-24}{3tgx-4}=0 \)
б) Укажите корни этого уравнения, принадлежащие отрезку \( [-\frac{π}{2};\frac{3π}{2}] \)
Решение
Найдем ОДЗ
\( tgx≠\frac{4}{3} \), по основному тригонометрическому тождеству( \( sin^2x+cos^2x=1/:cos^2x≠0 \)) \( tg^2=\frac{1}{cos^2x}-1 \), значит
\( cosx≠\frac{3}{5} \), значит \( sinx≠\sqrt{1-\frac{9}{25}}≠\frac{4}{5} \)
\( 2sinx*cosx≠\frac{24}{25} \)
Решаем уравнение
\( sin2x=\frac{24}{25} \)
\( 2x=arcsin\frac{24}{25}+2πn \) и \( 2x=π-arcsin\frac{24}{25}+2πn \)
\( x=\frac{arcsin\frac{24}{25}}{2}+πn \) и \( x=\frac{π}{2}-\frac{arcsin\frac{24}{25}}{2}+πn \)
Под ОДЗ подходит только один корень \( x=\frac{arcsin\frac{24}{25}}{2}+πn \)
б) Отберем корни на окружности
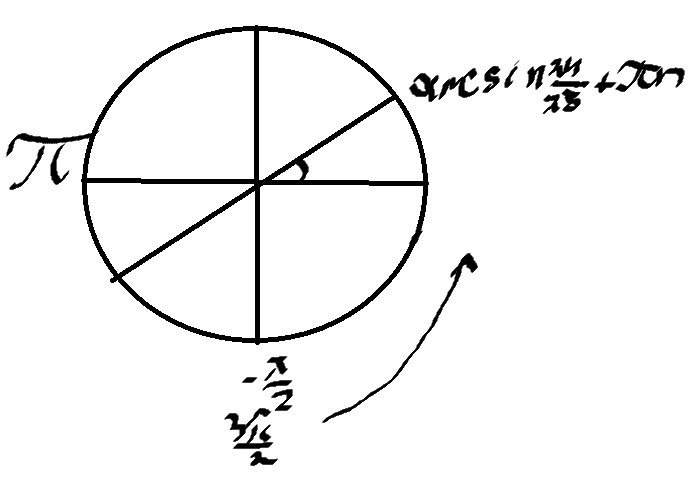
\( x=\frac{arcsin\frac{24}{25}}{2} \)
\( x=π+\frac{arcsin\frac{24}{25}}{2} \)
Ответ: а) \( x=\frac{arcsin\frac{24}{25}}{2}+πn \)б) \( x=\frac{arcsin\frac{24}{25}}{2} \), \( x=π+\frac{arcsin\frac{24}{25}}{2} \)
