а) Решите уравнение \( \frac{sin^2x+2sinx}{1-cosx}=2(1+cosx) \)
б) Укажите корни этого уравнения, принадлежащие отрезку \( [-\frac{π}{2};\frac{3π}{2}] \)
Решение:
ОДЗ: \( cosx≠1 \) и \( x≠2πn \)
\( sin^2x+2sinx=2(1-cosx)(1+cosx) \) преобразовываем
\( sin^2x+2sinx=2(1-cos^2x)=2-2cos^2x \)
\( sin^2x-2sinx=0 \) вынесем sinx
\( sinx(sinx-2)=0 \) найдем корни
\( sinx=0 \) значит \( x=πn \) НО УЧИТЫВАЕМ ОДЗ. \( x=π+2πn \)
\( sinx=2 \) нету решений, т.к область значений синуса [-1;1]
б) Отберем корни на окружности
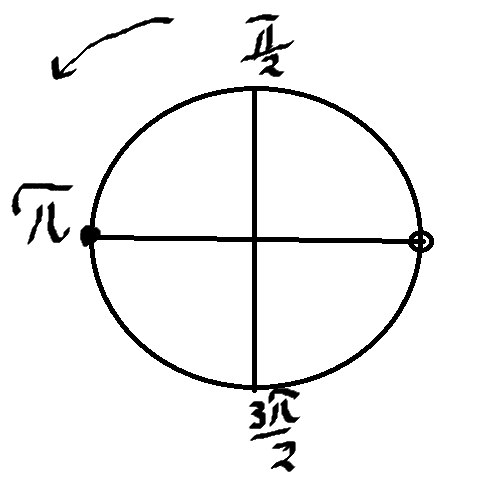
\( x=π \)
Больше корней нету
Ответ: a) \( x=π+2πn \) б) \( x=π \)
