а) Решите уравнение sinx+sin3x+|sin2x|=0
б) Укажите корни этого уравнения, принадлежащие отрезку \( [\frac{π}{2};2π] \)
Решение
Итак, я буду рассматривать два случая: Когда модуль раскроется со знаком + и наоборот.
Первый случай, когда \( sin2x⩾0 \) тогда \( 2πn≤2x≤π+2πn \)
\( πn≤x≤\frac{π}{2}+πn \) – при этих х, модуль раскрывается положительно, об этом не забываем. Погнали дальше
\( sinx+sin3x+sin2x=0 \) преобразуем \( 2sin2x*cosx+sin2x=0 \) вынесем sin2x
\( sin2x(2cosx+1)=0 \) – тогда получаем
\( sin2x=0 \) либо \( cosx=-\frac{1}{2} \)
\( x=\frac{πn}{2} \)
\( x=±\frac{2π}{3}+2πn \) под наше условие подходит только \( x=-\frac{2π}{3}+2πn \)
Второй случай, когда \( sin2x<0 \) , \( -π+2πn<2x<2πn \)
\( -\frac{π}{2}+πn<x<πn \) – это наше условие.
\( sinx+sin3x-sin2x=0 \) преобразуем \( 2sin2x*cosx-sin2x=0 \)
\( sin2x(2cosx-1)=0 \)
\( sin2x=0 \) либо \( cosx=\frac{1}{2} \)
\( x=\frac{πn}{2} \)
\( x=±\frac{π}{3}+2πn \) – под наше условие подходит только \( x=- \frac{π}{3}+2πn \)
Теперь отберем корни на окружности
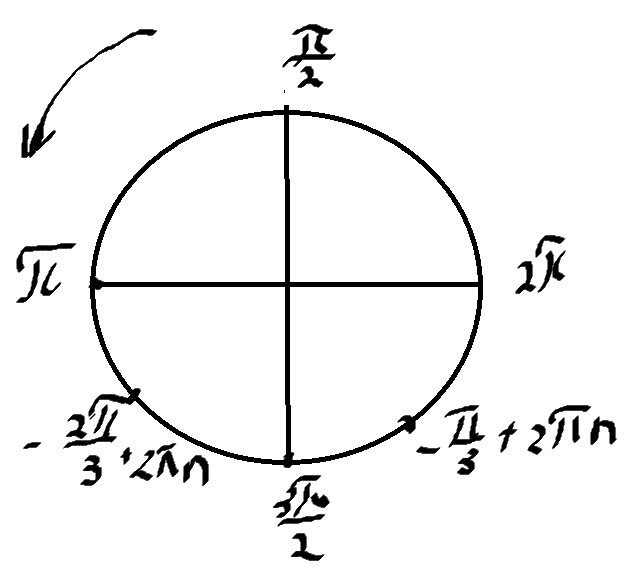
\( x=\frac{π}{2} \)
\( x=π \)
\( x=π+\frac{π}{3}=\frac{4π}{3} \)
\( x=\frac{3π}{2} \)
\( x=\frac{3π}{2}+\frac{π}{6}=\frac{10π}{6}=\frac{5π}{3} \)
\( x=2π \)
Если вам понравилось решение, то пожалуйста оставьте комментарий:) Мне будет очень приятно.
Ответик: \( x=\frac{πn}{2} \), \( x=-\frac{2π}{3}+2πn \), \( x=-\frac{π}{3}+2πn \) \( x=\frac{π}{2}, π, \frac{4π}{3}, \frac{3π}{2}, \frac{5π}{3}, 2π \)
