13. Дано уравнение \( log_{2}(sinx)*log_{sinx}(cos^2x)=-1 \)
А) Решите уравнение.
Б) Укажите корни этого уравнения, принадлежащие отрезку \( [4π;\frac{11π}{2}] \)
Стоит ли выкладывать дальше такие решение на 13 задачу или на листочке лучше? Ответьте пожалуйста в комментариях.
Пункт А
ОДЗ: (n-целый числа)
\( sinx>0 \) то есть \( 2πn<x<π+πn \) ( 1 и 2 четверть на тригонометрической окружности)
\( sinx≠1 \) то есть \( x≠\frac{π}{2}+πn \)
Решаем уравнение
Переходим к новому основанию 2
\( log_{2}(sinx)*\frac{log_{2}(cos^2x)}{log_{2}(sinx)}=-1 \) Сократим на логарифм, при этом
\( log_{2}(sinx)≠0 \) \( sinx≠1 \) – это в ОДЗ учтено
\( log_{2}(cos^2x)=-1 \)
\( cos^2x=\frac{1}{2} \) получаем что \( cosx=±\frac{\sqrt{2}}{2} \)
Получаем 4 серии корней
\( x=±\frac{π}{4}+2πn \)
\( x=±\frac{3π}{4}+2πn \)
Под ОДЗ подходит
\( x=\frac{π}{4}+2πn \)
\( x=\frac{3π}{4}+2πn \)
Пункт Б
Отберем корни на тригонометрической окружности (чтобы увеличить кликните по фотке)
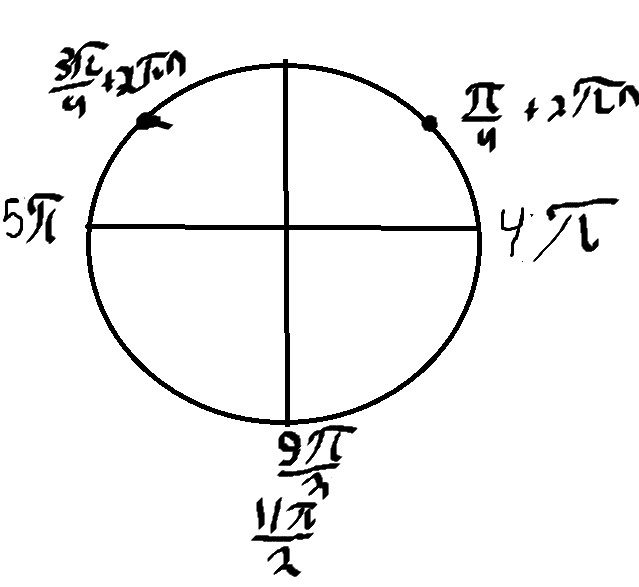
Получаем корни
\( x=4π+\frac{π}{4}=\frac{17π}{4} \)
\( x=4π+\frac{3π}{4}=\frac{19π}{4} \)
И записываем ответик:)
Ответ: а) \( x=\frac{π}{4}+2πn \) и \( x=\frac{3π}{4}+2πn \)б) \( x=\frac{17π}{4}, \frac{19π}{4} \) где n-целый числа
