Найдите сумму значений функции \( y=4cos^3x-3cosx \)в точках экстремума принадлежащих промежутку [0;11pi)
Решение
\( y’=0 \)
\( 12*cos^2x*(-sinx)+3sinx=0 \)
\( sinx(-12cos^2x+3)=0 \)
\( sinx=0 \), \( x=pi n \)
\( cosx=±\frac{1}{2} \),
Рассмотрим отрезок [0;2pi]
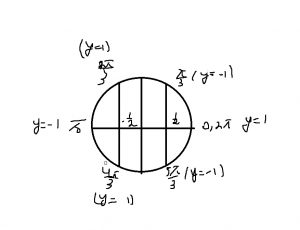
Видим, что сумма значений ф-ций в точках экстремума равна 0, соответственно на [2pi;4pi] будет аналогичная ситуация, …
Рассмотрим полуинтервал [10pi;11pi)
Т.к точка 11pi не включена, то в ней значение (y=-1 не будем считать)
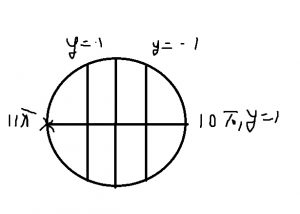
Значения ф-ции при \( x=\frac{31 \pi}{3} \) и \( x=\frac{32\pi}{3} \) сокращаются
Ответ: 1
