Вратарь выбросил мяч в поле, направив его под углом 45 к поверхности поля. Пока мяч не упал, высота, на которой он находится, описывается формулой \( h(t)=-5t^2+12t+1.25 \) ( h – высота в метрах, t – время в секундах, прошедшее с момента удара). Пренебрегая сопротивлением воздуха, считаем, что горизонтальная составляющая скорости мяча не меняется в полете. Определите, на каком расстоянии от вратаря в метрах мяч приземлится на поле.
Решение
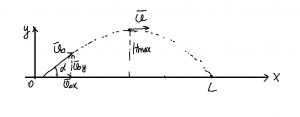
Нужны немного знания о физике. В задании не сказано чему брать ускорение свободного падения, но обычно на ЕГЭ берут \( 10 \) м/с^2
\( L=V_{0}*cos45*t_{полета} \)
Давайте найдет максимальную высоту полета \( h'(t)=-10t+12=0 \), откуда \( t{0}=1.2 \) время когда мячик долетит до макс высоты
Вспоминаем уравнение из физики \( v_{y}=v_{0y}t+g_{y}t \) или \( v_{y}=v_{0}sin45t-gt \)
В точке максимума будет только горизонтальная скорость, проекция скорости по Oy будет равна нулю
\( 0=V_{0}sin45-gt_{0} \)
\( V_{0}=\frac{gt_{0}}{sin45} \)
Осталось найти время полета
Мяч коснется земли, когда \( h(t)=0 \), откуда
\( t=2.5 \) – время полета
\( t=-0.1 \) – время отрицательным быть не может
\( L=\frac{gt_{0}}{sin45}*cos45t_{полета} \)
Подставляя все значения, получаем ответ
Ответ: 30
