В ящике с шоколадками \( \frac{2}{3} \)шоколадок содержит орехи, а \( \frac{5}{6} \)изюм. Сколько процентов шоколадок содержит и орехи, и изюм, если каждая шоколадка содержит хотя бы одну из добавок?
Решение
Пусть всего \( x \) шоколадок
Тогда \( \frac{2}{3}x \) – шоколадок с орехами и \( \frac{5}{6}x \) – шоколодак с изюмом.
\( \frac{1}{3}x \) – шоколодак без орехов и \( \frac{1}{6}x \) – шоколадок без изюма. Тогда
\( \frac{1}{3}x+\frac{1}{6}x \) – шоколадок без орехов и изюма
\( x-(\frac{1}{3}x+\frac{1}{6}x)=\frac{x}{2} \) – шоколадок и с орехами и с изюмом (половина или 50%)
Либо есть второй способ:
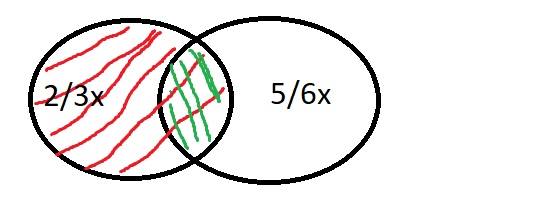
Шоколадок без изюма \( \frac{1}{6}x \), значит шоколодок и с изюмом и с орехом (зеленая область) \( \frac{2}{3}x-\frac{1}{6}x=\frac{x}{2} \)
Ответ: 50
