Докажем теорему: отрезок, соединяющий середины диагоналей равен половине разности оснований и лежит на средней линии.
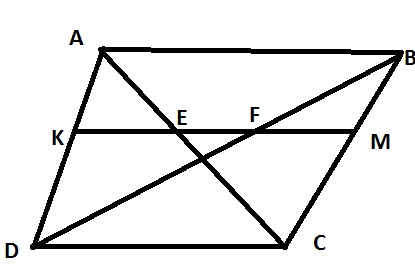
По т Фалеса получаем, что \( EF \) принадлежит \( KM \), значит параллельна основанияем.
\( KM=\frac{AB+DC}{2} \)
\( KE \) – средняя линия \( △ADC \)
\( KE=\frac{DC}{2} \)
\( FM \) – средняя линия \( △DCB \)
\( FM=\frac{DC}{2} \)
\( EF=KM-KE-FM \)
\( EF=\frac{AB+DC}{2}-\frac{DC}{2}-\frac{DC}{2}=\frac{AB-DC}{2} \)
ч.т.д
